打开文本图片集
摘要:地下隧洞的开挖引起原始地应力的重新分布,可能在围岩局部区域产生应力集中而导致围岩破坏。工程实际表明,即使在隧洞开挖过程中或开挖完成时,隧洞围岩保持稳定,隧洞在投入使用一段时间后,由于岩石强度的下降仍有可能引起隧洞围岩失稳。本文结合MSDPu强度准则和次临界裂纹生长理论详细推导了已知隧洞围岩任意一点应力状态,其达到破坏所需要的时间公式,并利用数值分析软件FLAC计算出圆形隧洞围岩顶点在不同原始地应力作用下达到破坏所需要的时间,为工程实际中隧洞围岩破坏预测提供参考。
关键词:隧洞围岩;强度准则;破坏时间;预测
1 引言
在漫长的地质年代里,地壳里的岩层已经形成了相对稳定的原始地应力场。由于交通运输、能源开发等原因,人们在浅地表或深地表开挖建造了各种各样的隧洞工程,扰乱了岩层原有的地应力场分布,使得隧洞围岩局部区域应力集中,从而引起隧洞围岩的破坏。已有的工程实例表明[1],即使在开挖过程中或开挖完成初期,隧洞没有发生失稳破坏的现象,由应力侵蚀、微裂纹拓展等原因引起的岩石强度下降,仍可能在隧洞运营一段时间之后造成围岩的局部失稳。如果能够对隧洞围岩的破坏时间进行预测判别,针对性的进行二次支护,避免或控制隧洞围岩的破坏,具有十分重要的意义。
目前,国内外的专家学者在隧洞围岩破坏预测方面已做了不少研究,并取得了一些成果。向天兵等[2]依据控制因素、破坏机制、发生条件3 个层次归纳出18种典型的围岩破坏模式,并进一步根据大型洞室群分步开挖过程中不断更新的工程地质条件和围岩性状,提出围岩破坏模式的动态识别、复核与调控方法,实现施工过程中围岩局部不稳定性问题的识别、预测与动态调控。戚承志等[3]利用不可逆热力学理论、连续相变形理论及弹塑性理论研究了深部隧洞围岩变形破坏的时间演化问题,给出了围岩分区破裂化现象的空间及时间解析解,并针对分区破裂化现象提出了一些支护方法。邓俏[4]等针对某地下金属矿山深井隔一采一方式回采过程形成的单面临空矿柱,运用 软件建立数值模拟模型,通过数值模拟,揭示矿柱及围岩的应力位移塑性区的变化情况,对回采过程中矿柱及围岩可能出现的破坏区域进行分析和预测。E.Z.Lajtai等[5]提出通过静定疲劳试验建立在特定应力状态下岩石试件达到破坏所需要的时间与所施加应力之间的曲线函数关系,来对岩石破坏时间进行预测。以上各种研究仅仅是对围岩可能出现的破坏模式或者破坏出现的位置进行预测,并没有对工程实际中比较关心的破坏时间进行预测。E.Z.Lajtai等提出的“静定疲劳法”虽然可以预测围岩的破坏时间,但这种方法需要进行大量的重复试验,并且假定两组对比试验的岩石强度一致,与实际情况存在一定差异。
本文结合MSDPu强度准则和次临界裂纹生长理论,提出通过数值模拟方法直接计算出隧洞围岩每一点的应力状态,并计算出该应力点达到破坏所需要的时间。
2 MSDPu强度准则
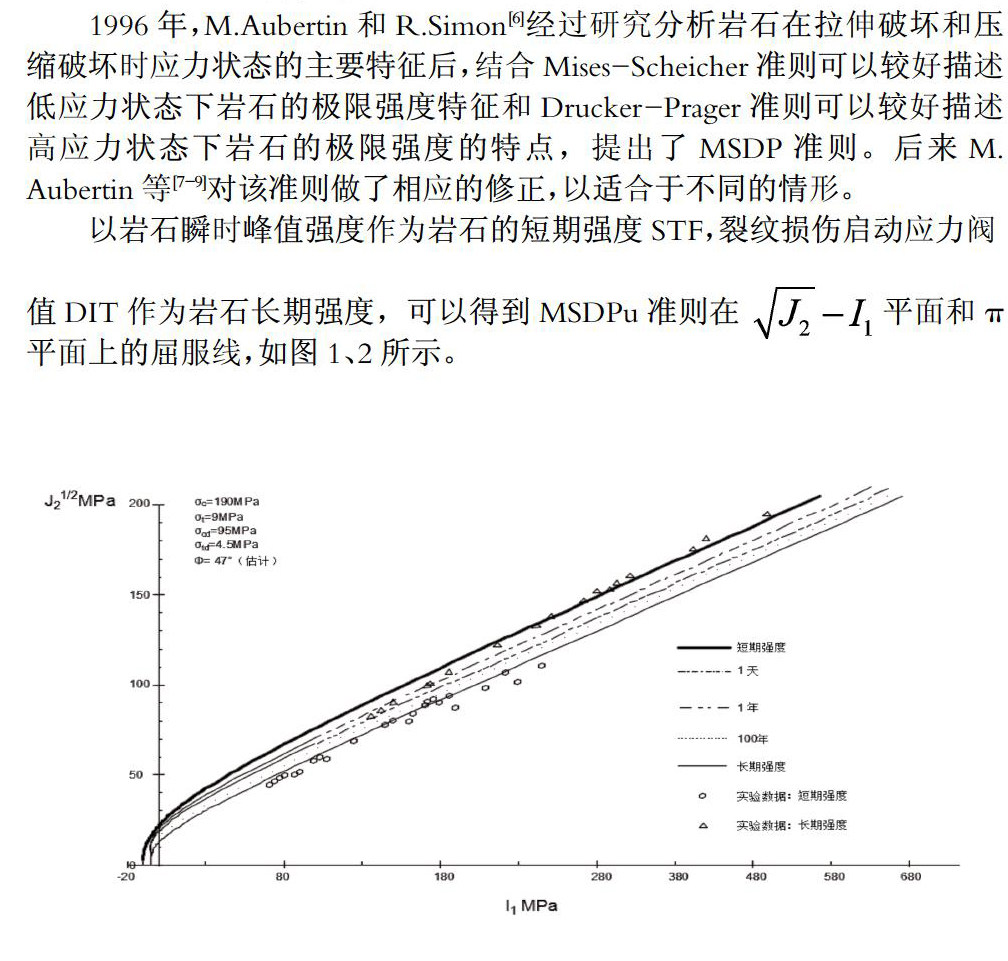
1996年,M.Aubertin和R.Simon[6]经过研究分析岩石在拉伸破坏和压缩破坏时应力状态的主要特征后,结合Mises-Scheicher准则可以较好描述低应力状态下岩石的极限强度特征和Drucker-Prager准则可以较好描述高应力状态下岩石的极限强度的特点,提出了MSDP准则。后来M.Aubertin等[7-9]对该准则做了相应的修正,以适合于不同的情形。
3次临界裂纹生长理论及破坏时间预测
对于一个给定的介于长、短期强度屈服面的应力状态,可以利用基于Charles定理拓展而来的次临界裂纹生长理论[10]来预测破坏发生的时间。通常认为微裂纹的形状为椭圆形,微裂纹端部的应力集中因子Ki与受到的外荷载、微裂纹几何尺寸相关。Charles对玻璃进行的静态疲劳分析研究和Atkinson[11]关于岩石断裂机理的分析研究表明,微裂纹端部的延伸速率V与应力集中因子Ki存在指数函数关系:
当K1≤K0时,破坏时间tf为无限长;当KI=KC时,tf等价于tr。根据相似类比的原则,可以利用与微观尺度相似的表达式等价宏观响应,即:
式中,β2为材料参数,σapp为所施加的偏应力。因此,当偏应力σapp等于短期强度STF时,tf等于参考时间tr;当偏应力σapp小于长期强度DIT时,破坏时间tf为无限长。公式(4-34)可以进一步改写为:
式中,δ1是施加的偏应力与长期强度 的差值,δ2是短期强度SFT与施加的偏应力的差值,α1和β为材料参数,对于花岗岩而言,α1=2.7s,β=9.73。Schmidtke和Lajtai[12]对花岗岩试件进行了单轴压缩静态疲劳试验,测得了不同加载荷载下试验发生破坏时间的数据。M.Aubertin[8]利用公式(19)对这些数据进行了拟合,其中长期强度取值短期强度的一半,得到拟合的效果比较吻合。
4 数值模拟计算中的数据处理
即可以根据其相应的长期强度DIT、短期强度SFT和所施加的偏应力σapp计算出其达到破坏的时间。一般的数值模拟分析软件如FLAC只能给出应力点的9应力分量,下面将对公式(19)所需要的主应力分量σ1、σ2、σ3和洛德角σ1、σ2、σ3进行推导。
4.1主应力σ1、σ2、σ3的确定
一点的应力状态在应力空间中可以由九个应力分量表示,在固定受力情况下,应力分量的大小与坐标轴方向有关。但无论坐标轴方向如何改变,主应力的数值是不变的。弹性力学中求解主应力的一元三次应力状态特征方程如式(20)所示,它的3个实根即为所求的3个主应力σ1、σ2、σ3。
5 算例
以一个圆形隧洞为计算模型,隧洞半径r=1m,围岩影响范围R=5m,并假定隧洞围岩应变沿轴向方向不变,即为平面应变问题,垂直方向应力与侧应力相等,即σv=σh。模型的位移边界条件和应力边界条件如图3、4。
隧洞围岩取为花岗岩,以瞬时峰值强度作为短期强度 ,以微裂纹损伤强度σcd作为长期强度 ,根据文献[]可知 的取值范围约为0.71~1,取 =0.71,隧洞围岩相应的材料参数如表1所示。
取隧洞围岩边界上顶点作为研究点,选取摩尔—库伦弹塑性本构模型作为隧洞围岩材料的本构模型,利用离散元软件FLAC可以计算得出该点在隧洞刚开挖完成时的应力状态,此时围岩的材料参数应取短期强度所对应的材料参数。随着原始地应力外荷载降低,隧洞围岩达到破坏所需要的时间呈指数迅速增加,并趋向于无穷。
6 结论
(1)结合MSDPu强度准则和次临界裂纹生长理论详细推导了已知隧洞围岩任意一点其应力状态时,其达到破坏所需要的时间的表达式。
(2)对圆形隧洞顶点的应力状态进行了数值模拟计算,并推导出由该点的应力状态的九个分量计算相应的主应力分量σ1,σ2,σ3的计算方程。
(3)在不同的原始地应力外荷载作用下进行数值模拟分析,得出随着原始地应力外荷载降低,隧洞围岩达到破坏所需要的时间呈指数迅速增加,并趋向于无穷的结论。
本文得到国家自然科学基金项目的资助,项目批准号:11172101
作者:吕爱钟(1961.3-),男,山东文登人,博士,华北电力大学教授,从事岩石力学的教学与研究;